- Optimización en biorreactores del medio para producción de células
- Optimización de Medios de Cultivo Celular para la Producción Máxima de Proteínas
- Optimización de Cultivos Microbianos para una Producción Máxima
- Diseño de experimentos y biorreactores (DoE)
- Comparación de métodos DoE para la optimización de la producción en biorreactores
Optimización en biorreactores del medio para producción de células
El objetivo de la optimización en biorreactores del medio también puede ser la producción de las células per se. La producción de materiales celulares a partir de colecciones de líneas celulares para fines de terapia celular son ejemplos de productos. Esto incluye el creciente interés por las células madre y sus células derivadas. Estas aplicaciones pueden aprovechar considerablemente la metodología DoE.
Así, la optimización de los medios de cultivo celular utilizando la metodología de diseño experimental es un enfoque atractivo para mejorar la eficiencia en el cultivo. Dong et al. aplicaron la metodología para refinar la composición de un medio de cultivo establecido para el crecimiento de la línea celular de hepatoma humano C3A. La selección de componentes nutritivos y factores de crecimiento se evaluó sistemáticamente según los procedimientos estándar de DoE. Los resultados del cribado de biorreactores indicaron que el factor de crecimiento de hepatocitos, la oncostatina M y el factor de crecimiento de fibroblastos-4 influyeron significativamente en las actividades metabólicas de la línea celular C3A. RSM reveló que los niveles óptimos para estos factores fueron 30 ng/ml de factor de crecimiento de hepatocitos y 35 ng/ml de oncostatina M. Experimentos adicionales en cultivos de hepatocitos humanos primarios mostraron una alta variabilidad en las actividades metabólicas entre células de diferentes individuos, lo que dificultó la determinación de niveles óptimos de factores. Sin embargo, fue posible concluir que el factor de crecimiento de hepatocitos, el factor de crecimiento epidérmico y la oncostatina M tuvieron efectos decisivos en las funciones metabólicas de los hepatocitos humanos primarios.
Se ha prestado mucha atención a los medios para la diferenciación y proliferación de células madre embrionarias. El hecho de que los medios de cultivo para la expansión de células madre contengan sustancias no definidas hace que la tarea sea exigente. Considerando el potencial para el trabajo clínico futuro con tales células, el uso de medios más bien definidos es altamente deseable. Por lo tanto, Knöespel et al., investigaron la composición detallada de un medio de cultivo químicamente definido sin suero para la expansión eficiente de células madre embrionarias de ratón (mESC). Comenzaron su estudio con un medio estándar sin suero con 11 factores adicionales (carnosina, cisteína, componentes C1, transferrina, suplemento de transferrina, factor de inhibición de la leucemia, insulina, BMP4, CaCl2, ZnSO4 y lípidos). El crecimiento de las células madre estuvo fuertemente influenciado por el equilibrio de los componentes del medio. El cribado utilizando un diseño de Plackett–Burman mostró que la insulina y el factor de inhibición de la leucemia tenían una influencia positiva significativa en la actividad proliferativa de las células, mientras que el zinc y la l-cisteína reducían el crecimiento celular. Una mayor optimización utilizando un diseño de «resolución mínima de carrera IV» mostró que el factor de inhibición de la leucemia era el principal factor para la supervivencia y proliferación de las células. Por lo tanto, los ensayos de cribado DoE son aplicables para desarrollar y refinar los medios de cultivo para células madre y también podrían emplearse para optimizar los medios de cultivo para células madre.
Se han llevado a cabo varios estudios de DoE sobre la diferenciación de células hematopoyéticas. Un ejemplo es la optimización de la eritropoyesis a partir de células de sangre de cordón umbilical humana (CD34+) hacia glóbulos rojos. Siete citoquinas (interleucina-3, interleucina-6, factor de células madre, eritropoyetina, factor estimulante de colonias, trombopoyetina y ligando Flt3) conocidas por afectar la maduración de producción de células rojas en humanos fueron seleccionadas para el cribado con un protocolo DoE. Se encontró que el factor de células madre (SCF) y la eritropoyetina (EPO) eran los factores más significativos en la producción de células rojas. La metodología ayudó a definir las características de diferenciación e interacciones de los factores SCF y EPO en la expansión total de células y la maduración de células de sangre de cordón umbilical hacia la línea eritroide, y delineó las concentraciones óptimas in vitro de cada citoquina (75 ng/ml y 4.5 unidades/ml, respectivamente). El cóctel de citoquinas optimizado aumentó 26,460 veces la expansión total de células y aceleró la maduración eritroide, obteniendo una pureza considerable de las células diferenciadas (más del 90% de células que expresan glicoforina-A). El uso de DoE se consideró efectivo y eficiente para el análisis, caracterización y optimización de la eritropoyesis in vitro y proporcionó una plataforma sistemática para el uso de otros factores de crecimiento para la expansión in vitro de productos celulares.
Además, Panuganti et al. aplicaron un diseño para la producción de células de fracciones factoriales completas (FFD) con células madre y progenitoras hematopoyéticas cultivadas con una variedad de citoquinas (por ejemplo, interleucina-3, interleucina-6, interleucina-9, factor de células madre de alta o baja dosis, junto con trombopoyetina e interleucina-11) para promover la diferenciación en células megacariocíticas, los precursores de las plaquetas. El estudio demostró que un proceso de cultivo de tres fases con aumento de pH y pO2 y diferentes cócteles de citoquinas incrementa enormemente la producción de megacariocitos. Por lo tanto, este estudio muestra claramente los beneficios de desentrañar la complejidad del proceso de diferenciación de células madre mediante DoE.
Optimización de Medios de Cultivo Celular para la Producción Máxima de Proteínas
La industria biotecnológica depende en gran medida de cultivos celulares de mamíferos para producir productos esenciales como anticuerpos y enzimas. Estos cultivos requieren una receta específica, o medio, para prosperar y producir las proteínas deseadas. Tradicionalmente, descubrir la composición óptima del medio era un proceso lento de prueba y error. Sin embargo, un nuevo enfoque llamado Diseño de Experimentos (DoE) está cambiando el juego.
DoE es un método estadístico que ayuda a los investigadores a planificar estratégicamente experimentos para optimizar múltiples factores simultáneamente. Esto es particularmente útil para formulaciones de medios complejos utilizados en cultivos celulares de mamíferos, que a menudo contienen muchos ingredientes.
Por qué el DoE es Perfecto para la Optimización de Medios de Cultivo Celular
- Interacciones Complejas: A diferencia de los cultivos microbianos más simples, los medios para células de mamíferos tienen muchos ingredientes que interactúan entre sí. DoE nos ayuda a comprender estas interacciones e identificar los componentes más influyentes.
- Maximizar el Rendimiento: El objetivo suele ser maximizar la producción de proteínas. DoE permite a los investigadores identificar eficientemente la combinación ideal de nutrientes para la productividad máxima de las células.
DoE en Acción: Un Estudio de Caso con Anticuerpos Monoclonales
Los anticuerpos monoclonales son un ejemplo primordial de proteínas producidas en cultivos celulares de mamíferos. Los investigadores Sen y Roy-Choudhury utilizaron DoE para optimizar el medio para una línea celular hibridoma que produce un anticuerpo específico.
- Paso 1: Identificación de los Elementos Clave: Comenzaron probando una gran cantidad de componentes del medio para identificar los más críticos para la producción de anticuerpos. Esta selección identificó siete ingredientes clave, incluyendo glucosa, suero y aminoácidos específicos.
- Paso 2: Encontrar el Equilibrio Perfecto: Luego se utilizaron técnicas de DoE para determinar la concentración óptima de cada uno de estos siete componentes. ¿El resultado? Un medio de cultivo que más que duplicó tanto la cantidad como la productividad específica del anticuerpo deseado en comparación con la receta original.
DoE para la Optimización de Alto Rendimiento
Otro estudio realizado por Rouiller et al. demuestra el poder del DoE para la optimización de medios a gran escala. Utilizaron un enfoque de alto rendimiento para mejorar un medio para producir proteínas terapéuticas en células de ovario de hámster chino (CHO).
- Pruebas de Cientos de Combinaciones: Crearon cientos de mezclas de medios variando la concentración de 43 componentes diferentes. Estas mezclas se probaron en un solo experimento para identificar las combinaciones más efectivas.
- Potencia de Análisis de Datos: Se utilizaron métodos estadísticos avanzados para analizar la gran cantidad de datos generados. Esto ayudó a identificar los factores clave que influyen en la producción de proteínas y, en última instancia, condujo a una formulación de medio significativamente mejorada.
El Futuro del DoE en el Diseño de Medios de Cultivo Celular
El DoE está convirtiéndose rápidamente en una herramienta esencial para optimizar los medios de cultivo celular en la industria biotecnológica. Su capacidad para manejar interacciones complejas e identificar factores clave está llevando al desarrollo más rápido de formulaciones de medios eficientes, acelerando así la producción de proteínas que salvan vidas.
El DoE ofrece un enfoque poderoso para optimizar los medios de cultivo celular, lo que conduce al desarrollo más rápido de formulaciones de medios eficientes para la producción de proteínas en la industria biotecnológica.
Optimización de Cultivos Microbianos para una Producción Máxima
Cultivos Microbianos Para Producción son una potencia para producir una amplia gama de productos, desde biocombustibles hasta enzimas.
Pero para aprovechar al máximo estas pequeñas fábricas, necesitamos optimizar su entorno: el medio de cultivo.
Esta publicación de blog se adentra en el mundo de la optimización de medios y cómo puede aumentar significativamente la producción microbiana.
Metabolitos Primarios: Impulsando el Crecimiento y Más Allá
Una clase de productos microbianos son los metabolitos primarios, esenciales para su crecimiento y supervivencia.
Pero algunos microbios pueden ser superestrellas, produciendo grandes cantidades de estos metabolitos para nuestro beneficio.
La optimización del medio juega un papel crucial en este proceso.
Por ejemplo, la producción de alcoholes mixtos por una cepa de Clostridium.
Aquí, el Diseño de Experimentos (DoE) ayudó a diseñar un medio específicamente para este propósito. El glicerol fue la fuente de carbono elegida, complementada con otros componentes clave identificados mediante un cribado de un factor a la vez.
Un diseño modificado de Taguchi ajustó entonces las concentraciones de estos componentes, llevando a una composición de medio óptima.
¡Este medio optimizado condujo a una impresionante producción de 17.7 g/L de alcoholes mixtos en un biorreactor, superando las predicciones del modelo!
Metabolitos Secundarios: Revelando un Potencial Oculto
Los cultivos microbianos para producción también pueden producir una amplia gama de metabolitos secundarios, a menudo con propiedades únicas.
El rhamnolípido, un biosurfactante producido por Pseudomonas aeruginosa, es un ejemplo.
Usando DoE, los investigadores examinaron varias respuestas, incluida la reducción de la tensión superficial y la actividad de emulsificación.
¡El medio no optimizado produjo apenas 0.3 mg/mL de rhamnolípido, pero la optimización del medio utilizando DoE llevó a un aumento notable de 15 veces! Esto destaca el inmenso potencial de la optimización del medio para desbloquear tesoros ocultos de los microbios.
Proteínas: Los Caballos de Batalla de la Biotecnología
Los cultivos microbianos también son campeones en la producción de proteínas, incluidas valiosas proteínas recombinantes.
Un estudio exploró la influencia de la composición del medio en la producción de lisozima por Aspergillus niger. Factores como el almidón, la peptona y el sulfato de amonio fueron identificados como críticos.
A través de una combinación de técnicas de optimización, se formuló una composición de medio que resultó en un rendimiento de lisozima de 209 g/L, muy cerca del máximo teórico.
Más Allá de lo Básico: Ajustando Fino la Maquinaria Celular
La optimización del medio puede ir más allá de simplemente aumentar la producción.
Por ejemplo, los investigadores utilizaron un experimento de diseño factorial completo para optimizar el patrón de glicosilación de una proteína producida por Pichia pastoris.
Aunque lograron la glicosilación máxima, esto se logró a expensas de la producción total de proteínas. Esto muestra el potencial de la optimización del medio para ajustar finamente la maquinaria celular para objetivos específicos.
La optimización del medio es una herramienta poderosa para desbloquear todo el potencial de los cultivos microbianos.
Desde metabolitos primarios hasta proteínas complejas, optimizar el medio puede aumentar significativamente la producción, mejorar la calidad del producto e incluso influir en funciones celulares específicas.
A medida que la investigación en esta área continúa, podemos esperar aún más descubrimientos y aplicaciones emocionantes del fascinante mundo de los microbios.
Diseño de experimentos y biorreactores (DoE)
Muy a menudo, las aplicaciones de diseño de experimentos y biorreactores se extienden más allá del simple diseño y optimización de los medios, por ejemplo, cuando se incluyen otros factores como variables del proceso físico (por ejemplo, agitación y temperatura).
Objetivo principal
El objetivo típico en la mayoría de los ejemplos es identificar una mejor selección y composición cuantitativa de los componentes del medio para maximizar la producción y la economía del proceso.
Esto se hace principalmente utilizando el título del producto, la concentración final, el rendimiento o la productividad como respuesta de DoE en el diseño.
Aún así, una métrica de respuesta aún mejor podría ser el costo del medio de producción por volumen de producto objetivo, u otras combinaciones de parámetros de costos en el proceso de producción, como el efecto en el costo de separación y purificación, el costo de mano de obra versus la cantidad de producto objetivo, etc.
Énfasis Actual en la Literatura
Sin embargo, hasta ahora, los informes que aparecen en la literatura actual se han centrado en la mayoría de los casos en el rendimiento y la productividad del producto objetivo.
Medios para la producción de metabolitos y proteínas en cultivos microbianos
La producción de metabolitos y proteínas en un cultivo de biorreactor microbiano son las aplicaciones más típicas de diseño de experimentos y biorreactores.
Los objetivos de estos procesos coinciden con el objetivo general descrito anteriormente.
Ejemplo: Producción de Ácido Clavulánico
Debido al uso amplio y a largo plazo, así como a los márgenes ajustados de costos de producción, muchos de los ejemplos de DoE informados en la literatura involucran la parte de fermentación en la fabricación de antibióticos.
Un ejemplo típico es la producción del ácido clavulánico antibiótico a partir de Streptomyces clavuligerus.
En un estudio de DoE de 2005 realizado por Wang et al., la composición del medio se optimizó primero mediante el cribado de una variedad de ingredientes del medio en un FFD de dos niveles de Plackett-Burman (2n), al que posteriormente siguió la determinación de los niveles óptimos de los componentes del medio seleccionados por RSM.
En el cribado inicial mediante experimentos FFD, se identificó la harina de soja en polvo, FeSO4⋅7H2O y la ornitina como los factores más influyentes, mientras que el fosfato de potasio y el fosfato de magnesio no lo fueron, en términos del rendimiento de ácido clavulánico.
Determinación de Niveles Óptimos de Componentes del Medio Seleccionados por RSM
En el modelo RSM en biorreactores utilizado posteriormente basado en un diseño CCC, se determinaron las concentraciones óptimas de estos tres factores para el mayor rendimiento de ácido clavulánico (la concentración óptima de harina de soja en polvo se determinó como 38,10 g l − 1, FeSO4⋅7H2O como 0,395 g l − 1 y ornitina como 1,18 g l − 1.
El factor de correlación fue de 0,98 y el coeficiente de variación fue del 6,6%. Al ejecutar la fermentación antibiótica con estos ajustes en un lote de 72 h, el rendimiento del producto aumentó en un 50%.
Por lo tanto, simplemente utilizando el protocolo DoE estándar como se describió anteriormente, se logró una mejora profunda de la productividad de la producción.
El costo de I + D para lograr este resultado se puede estimar como muy bajo en comparación con su efecto.
Por supuesto, una nueva composición de medio de producción requerirá una mayor verificación, ampliación y validación adicional seguida de esfuerzos regulatorios debido a los requisitos para los medicamentos farmacéuticos.
Comparación de métodos DoE para la optimización de la producción en biorreactores
En el siguiente texto, se hace referencia a una serie de métodos comunes de diseño DoE, como los métodos de Plackett-Burman, Taguchi, Box-Behnken y Box-Wilson. Estos cuatro diseños se explican brevemente a continuación; sin embargo, en la práctica habitual también se aplican otros enfoques de diseño similares o equivalentes.
Método de Plackett-Burman
Descripción
Este método se refiere al trabajo original de 1946 de Plackett y Burman, donde presentaron diseños experimentales para investigar la dependencia de la cantidad medida en un número de variables o factores independientes. En este trabajo, describen los diseños factoriales de dos niveles donde el número de experimentos es un múltiplo de 4. Discuten en particular los principios básicos de DoE donde se prueban L niveles en un número limitado de experimentos para minimizar la varianza de las estimaciones de estas dependencias. Sin embargo, las interacciones entre los factores se consideraron insignificantes.
Solución
La solución a este problema es encontrar un diseño experimental donde cada combinación de niveles para cualquier par de factores aparezca el mismo número de veces, a lo largo de todas las corridas experimentales. Un diseño factorial completo cumpliría con este criterio, pero la idea es encontrar diseños más pequeños.
Comparación de métodos DoE para la optimización de la producción en biorreactores
Aqui se presenta una comparación de métodos DoE para la optimización de la producción en biorreactores. Es importante seleccionar el método DoE adecuado en función de los objetivos específicos del estudio y de las limitaciones experimentales.
Método de Taguchi
Descripción
El método es similar al método de Plackett-Burman en su versión básica y propone varios enfoques para diseños experimentales que utilizan FFD de dos, tres y niveles mixtos. El método Taguchi se describe ocasionalmente en la literatura como un método de control de calidad porque ese era el propósito original del método. En algunos casos, el método se puede utilizar en línea mientras se ejecuta el proceso. Taguchi ha publicado varias guías para aplicar los métodos de diseño.
Aplicaciones
Este método se utiliza en una amplia gama de industrias, incluyendo la fabricación, la electrónica y la industria alimentaria.
Comparación de métodos DoE para la optimización de la producción en biorreactores
El método Taguchi ofrece una serie de ventajas sobre otros métodos DoE, incluyendo su simplicidad, eficiencia y robustez. Sin embargo, también tiene algunas limitaciones, como su incapacidad para modelar interacciones complejas entre factores.
Método de Box-Wilson
Descripción
Éste es en principio equivalente a un CCD común como se describió anteriormente. El método de Box-Wilson investiga el impacto de las variables experimentales en la salida de respuesta que utilizan CCD para utilizar un diseño de superficie de respuesta, que se elige comúnmente para la optimización de la respuesta. Box y Wilson sugirieron el uso de un modelo polinomial de segundo grado.
Aplicaciones
Este método se utiliza en una amplia gama de aplicaciones, incluyendo la química, la ingeniería y la ciencia de los materiales.
Comparación de métodos DoE para la optimización de la producción en biorreactores
El método Box-Wilson es una poderosa herramienta para la optimización de procesos complejos. Sin embargo, puede ser computacionalmente intensivo y requerir un gran número de experimentos.
Método de Box-Behnken
Descripción
Se refiere a los diseños experimentales para RSM descritos por Box y Behnken. En el método, cada factor se coloca en uno de tres valores igualmente espaciados, generalmente codificados como -1, 0, +1. El diseño también debe ser suficiente para ajustar un modelo cuadrático. La relación entre el número de puntos experimentales y el número de coeficientes en el modelo cuadrático debe ser razonable. La varianza de estimación debería depender más o menos solo de la distancia del centro y no debería variar demasiado dentro del cubo más pequeño que contiene los puntos experimentales. Los diseños de Box-Behnken se consideran eficientes en cuanto a la cantidad de experimentos necesarios.
Aplicaciones
Este método se utiliza en una amplia gama de aplicaciones, incluyendo la química, la ingeniería y la ciencia de los materiales.
Comparación de métodos DoE para la optimización de la producción en biorreactores
Los diseños Box-Behnken son una opción eficiente para la optimización de procesos con un número moderado de factores. Sin embargo, no son tan eficientes como los diseños factoriales completos
| Método DoE | Descripción | Utilidad |
| Diseño de Plackett-Burman | Diseños fraccionarios de dos niveles para estudiar k=N-1 variables en N corridas, donde N es un múltiplo de 4. Los diseños de mayor número de N son diseños no geométricos. Los niveles se presentan a menudo como (+) y (-), y los valores se varían sistemáticamente en un plan experimental. Los diseños P-B se llevan a cabo típicamente como diseños de Resolución III o IV (2k-P, 21k-P). | Los diseños P-B de resolución III y IV se aplican comúnmente cuando se criban un gran número de componentes de medios (ver detalles en las Tablas 15.2-15.5). En particular, cuando el medio contiene >20 componentes, la reducción de la resolución ahorra mucho trabajo. |
| Diseño de Taguchi | Una alternativa similar al diseño PB basada en tablas con nivel (1) y nivel (2). Los diseños simples de Taguchi son muy similares a los diseños PB, pero también podrían extenderse a más niveles. | Los diseños de Taguchi, siendo comúnmente aplicados en el control de calidad industrial, son preferidos en el diseño de medios. Debido a su adaptación a muchos parámetros de calidad, también es muy útil en el diseño de medios de cultivo con muchos componentes. |
| Diseño de Box-Behnken | Diseños de tres niveles para su uso con superficies de respuesta. Los diseños BB se forman combinando factoriales de 2k con diseños de bloques. | Los diseños BB permiten reducir el número de experimentos. Como el diseño de medios podría beneficiarse de las pruebas a más de dos niveles de concentración, esto es muy útil. |
| Diseño de Box-Wilson | Un diseño equivalente con un CCD común como se describió anteriormente con puntos centrales que se aumentan con un grupo de «puntos estrella» que permite la estimación de la curvatura. |
Evaluación del Diseño Experimental en biorreactores.
En la una evaluación del diseño experimental en biorreactores vez que los experimentos han sido llevados a cabo de acuerdo al plan de diseño experimental y los resultados de las variables de respuesta han sido compilados, se utiliza la regresión lineal múltiple (MLR, por sus siglas en inglés).
El propósito de la MLR es evaluar si el espacio experimental ha sido diseñado de manera ortogonal y si permanece igual después de que los experimentos han sido realizados.
En la MLR, el modelo matemático describe una relación entre una o más variables independientes y una variable de respuesta como Yi = 𝛽0 + 𝛽1Xi1 + 𝛽2Xi2 + · · · + 𝛽p Xip + 𝜀i donde i = 1,2, … ,n.
Las interacciones más complejas debido a la covariación se describen mediante términos lineales o cuadráticos.
Sin embargo, los términos de interacción u otros términos complejos deben evaluarse para ver si ofrecen contribuciones aceptables al modelo en comparación con la incertidumbre de la contribución (relación señal-ruido).
En la evaluación del diseño experimental en biorreactores de la contribución de cada coeficiente y la posterior optimización del modelo, el objetivo es reducir el factor de desviación del modelo 𝜀i.
Al caracterizar una superficie de respuesta, los términos de covariación describen su asimetría, mientras que los términos cuadráticos describen su curvatura.
En un diseño completo, debido al número de grados de libertad, es probable que los términos que describen la interacción y la curvatura puedan incluirse en el modelo MLR.
Al evaluar un FFD mediante MLR, es práctica común respaldar los términos lineales con un número limitado de términos complejos.
En un FFD, dichos términos a menudo están confundidos entre sí.
Si el diseño no es ortogonal, la regresión de mínimos cuadrados parciales (PLS) es una mejor alternativa.
Este método evaluación del diseño experimental en biorreactores también puede ser utilizado cuando hay varias respuestas correlacionadas en el conjunto de datos.
PLS puede proporcionar entonces un método de evaluación más robusto que es útil incluso si hay un número limitado de datos faltantes en la matriz de respuesta.
Las evaluaciones del modelo en las aplicaciones de diseño en los medios discutidas o citadas a continuación son en su mayoría ejemplos de estos procedimientos analíticos.
Para un caso con cinco factores, necesitamos ya sea 16 (25−1) o 8 (25−2) factores en los experimentos.
El último diseño se utiliza principalmente en pruebas de robustez, donde se prueba la sensibilidad de la variación de la variable de respuesta en un conjunto reducido de experimentos alrededor de un óptimo de la variable de respuesta.
La variación de las variables generalmente se realiza en pasos muy pequeños alrededor de un campo específico de interés, como una composición preferida de un medio de cultivo, para evaluar la estabilidad del proceso.
Comúnmente, el modelo se valida mediante dos residuos diagnósticos.
El primero de estos, el valor R2, es la fracción de la variación de las respuestas que puede ser explicada por el modelo.
Esto describe la bondad de ajuste, o qué tan bien pueden ser reproducidas las ejecuciones actuales en un modelo matemático.
El otro residuo, el valor Q2, es la fracción de la variación de la respuesta predicha por el modelo según la validación cruzada.
Esto describe la bondad de predicción, o qué tan bien pueden predecirse nuevos experimentos utilizando el modelo matemático.
Las pruebas de R2 y Q2 a veces son descuidadas, lo que desafortunadamente reduce la posibilidad de apreciar completamente los resultados.
Los valores típicos que indican una buena calidad de robustez son R2 > 0.75 y Q2 > 0.75. Los valores inferiores a 0.25 normalmente se considerarían inútiles.
Diseño de experimentos de cribado en biorreactores

En el diseño de experimentos en biorreacotres la aproximación más eficiente para comenzar un nuevo medio de biorreactor es mediante experimentos de cribado de los componentes de dicho medio considerados importantes para la capacidad del mismo.
Estos diseño de experimentos en biorreacotres de cribado deben realizarse desde esquinas seleccionadas en el espacio experimental. El procedimiento se conoce comúnmente como un diseño factorial fraccionado (FFD) porque solo se investiga una fracción de los posibles valores de las esquinas en el espacio de diseño.
Las tres variables de factor seleccionadas se someten a prueba en dos niveles de valores, y cada variable se prueba dos veces a niveles bajos y altos. En la optimización del diseño del medio, las tres variables podrían ser tres componentes clave de nutrientes a dos niveles de concentración cada uno.
Este primer paso del plan de Diseño de Experimentos en biorreactores (DoE) requiere una cuidadosa consideración basada en la experiencia previa. Puede ser que los protocolos de cultivo ya hayan establecido variables de factor bien definidas, como la concentración de componentes en el medio y la configuración de variables de estado en el fermentador. Sin embargo, la selección de variables y sus niveles depende completamente del juicio del experimentador y del conocimiento previo sobre el proceso estudiado. Elecciones inapropiadas limitarán la utilidad de los resultados, haciendo necesario llevar a cabo nuevos diseño de Experimentos en biorreactores con otras variables y niveles.
Top of Form
Bottom of Form
El número de diseño de experimentos en biorreacotresen un diseño factorial fraccionado (FFD) de dos niveles se puede describir matemáticamente como 2^n-k, donde n es el número de factores que se investigarán a niveles bajos y altos, y k es el número de pasos para reducir el diseño experimental. Si, por ejemplo, participan cinco variables en el experimento, terminará con 16 (2^5-1) o 8 (2^5-2) experimentos, respectivamente, dependiendo de cuántos pasos se reduzca el diseño.
Sin embargo, en la práctica actual, este procedimiento rara vez se realiza de manera sistemática; en cambio, se elige un nivel de reducción apropiado. El cribado se mejora mediante réplicas en el punto central del dominio experimental, con el propósito de recopilar valores adicionales de respuesta y, al mismo tiempo, determinar el error experimental para la respuesta. La reducción de diseño de experimentos en biorreacotres de factores disminuye la calidad estadística del cribado. Esto será evidente en los parámetros de rendimiento estadístico de bondad de predicción y bondad de ajuste. El conjunto completo de experimentos debe realizarse en un orden aleatorio para evitar errores sistemáticos. Una causa típica de errores sistemáticos es cuando se realizan tres experimentos en el punto central de un diseño uno tras otro utilizando el mismo procedimiento experimental.
Por lo tanto, la aleatorización debe aplicarse para ocultar al experimentador los resultados esperados, ya sean buenos o malos. El resultado típico de un experimento de cribado para medios de cultivo es la identificación de algunos componentes importantes en el medio. Estos componentes deben ser investigados más a fondo en un nuevo diseño experimental con el propósito de determinar los valores óptimos de los factores. Esto requiere un plan experimental más elaborado, como un diseño central compuesto en caras (CCF) o un diseño central compuesto circunscrito (CCC).
En el caso del CCF, se incluyen valores adicionales (por ejemplo, concentraciones) de las variables en los puntos centrales de la superficie entre las esquinas del espacio experimental. En el CCC, estos se desplazan fuera del espacio a la misma distancia desde el punto central que la distancia desde el punto central hasta las esquinas. Teóricamente, el diseño CCC es algo mejor que el diseño CCF porque cubre un volumen más grande en el espacio de diseño.
Los resultados de los diseño de Experimentos en biorreactores CCF o CCC se representan en un gráfico de contorno o en una superficie de respuesta donde se visualiza claramente el óptimo. Este último paso también ha dado nombre al procedimiento comúnmente conocido como la metodología de superficie de respuesta (RSM, por sus siglas en inglés).
Debería enfatizarse que tanto variables cuantitativas como cualitativas pueden incluirse entre los factores, al igual que factores multiniveles cuantitativos y cualitativos. Por ejemplo, en un caso con dos factores cualitativos, X1 (con cuatro niveles discretos) y X3 (con tres niveles discretos), y un factor cuantitativo, X2, se puede generar un diseño como se muestra en la Figura 15.6. Sin embargo, en este caso, no es posible utilizar puntos centrales entre los niveles discretos de los factores X1 y X3. En su lugar, un punto central puede posicionarse en uno de los niveles discretos de las variables cualitativas o en un nivel intermedio de la variable cuantitativa. Un ejemplo típico en el diseño de medios es cuando se comparan dos alternativas diferentes de componentes de medios.
Diseño de experimentos de biorreactores para el desarrollo y optimización de medios .

El diseño de experimentos de biorreactores (DoE) se ha convertido en una metodología ampliamente aceptada para investigar las relaciones estadísticas entre las variables de entrada y salida de sistemas técnicos.
Los sistemas de procesos y producción, donde tienen lugar transformaciones físicas, químicas o biológicas, pueden beneficiarse sustancialmente mediante el uso de DoE como una herramienta de diseño y optimización.
En particular, los bioprocesos con la exigente tarea de diseñar medios de cultivo complejos para biorreactores han podido aprovechar en gran medida esto.
En la planificación de experimentos de biorreactores para evaluar y optimizar la composición de un medio de producción, la metodología DoE es particularmente útil para evitar sesgos experimentales y reducir significativamente el número necesario de experimentos de biorreactores.
Los procedimientos para aplicar la metodología DoE al diseño de medios son directos.
Se investigan factores de entrada definidos, como mezclas y concentraciones de componentes del medio, añadidos a un cultivo en transformación, a partir del cual se obtienen factores de salida o respuestas, como la concentración y tasas de formación de la(s) molécula(s) o células objetivo u otras entidades de importancia.
Sin embargo, la fortaleza de DoE radica en que también revela cómo las interacciones entre los factores de entrada (es decir, los componentes del medio o posiblemente también otros parámetros del proceso) influyen en las respuestas de salida.
Estas interacciones a menudo son difíciles de descubrir e interpretar con otros métodos experimentales.
Sin embargo, la conversión en un biorreactor y en su medio de cultivo es más compleja que un equilibrio entre factores de entrada y salida.
La mayoría de los insumos ejercen sus efectos como una carga inicial de efectos múltiples sobre el bioproceso en transformación.
Sin embargo, cualquier persona con experiencia en bioprocesamiento es consciente de que las acciones y efectos se desplazan en el tiempo durante un procedimiento de cultivo.
Algunos factores se establecen desde el principio del proceso, mientras que otros aparecen más tarde, por ejemplo, al alimentar componentes del medio en ciertos momentos o períodos.
El inicio de cambios en el metabolismo causados por la activación o desactivación de componentes, como factores de crecimiento, vitaminas y agentes estresantes microbianos, complica aún más el curso de los eventos en el proceso.
En bioprocesos recombinantes, la inducción de la expresión de una proteína recombinante es otro parámetro dependiente del tiempo de importancia.
Además, los factores del medio se combinan con parámetros operativos del proceso como la temperatura, la agitación y la aireación.
Por lo tanto, las interacciones entre los parámetros del medio son muy relevantes para investigar; la metodología DoE nos permite hacerlo.
Fundamentos de la Metodología de Diseño de Experimentos de biorreactores.
La fortaleza de la metodología DoE, en comparación con los métodos de optimización que varían una variable a la vez, radica en que se puede lograr un resultado confiable con solo unos pocos experimentos de biorreactores.
En DoE, se puede evaluar la dirección más favorable para moverse en el espacio de diseño factorial y encontrar un óptimo real.
Es posible quedar atrapado en un cuasi-óptimo al variar solo una variable a la vez, incluso en el caso de dos variables al mantener constante la variable X1; se realizan cinco experimentos de biorreactores variando la variable X2.
A partir del óptimo obtenido, luego se varía la variable X1 en otros cuatro experimentos. Nunca se alcanza un óptimo correcto porque hay una dependencia entre las dos variables.
En cambio, al variar simultáneamente tanto X1 como X2 y analizar el resultado con procedimientos DoE, se puede revelar la dirección del óptimo real.
Al optimizar medios de cultivo o realizar otros estudios de optimización de bioprocesos, este enfoque es claramente preferible, ya que con un enfoque de una sola variable es probable que el experimentador termine en concentraciones de medios cuasi-óptimas.
Cromatografía líquida de alta resolución en línea

Cromatografía líquida de alta resolución en línea para la estimación de subproductos de la fermentación mixta de ácidos.
El sensor virtual en la cromatografía líquida utiliza una sonda NIR in situ con una ventana de longitud de onda fija para adquirir una señal de absorbancia que está relacionada con la concentración total de biomasa. Esta señal se combina con datos de un HPLC en línea, donde los picos del cromatograma se analizan para metabolitos seleccionados en el medio, siendo importantes para supervisar el estado metabólico de la cultura de E. coli que expresa la proteína.
Después de la evaluación de las áreas de los picos, los datos de HPLC se convierten en concentraciones de acetato, glucosa, lactato y formiato. Al transformar las señales de HPLC y biomasa a concentraciones específicas (g de metabolito/g de célula por hora), se monitorea el estado fisiológico y se utiliza para determinar la tasa de alimentación en el cultivo por lotes alimentado.
La ventaja en este caso es que la instrumentación en el sensor virtual está bien establecida, y los métodos robustos y el HPLC analizan varios analitos por corrida. La desventaja es el tiempo de espera relativamente largo del HPLC (hasta 25 minutos) en comparación con la sonda NIR, que responde en segundos.
En particular, este enfoque de sensor virtual brinda la oportunidad de controlar el desbordamiento metabólico de la fermentación de ácidos mixtos y el metabolismo de desbordamiento de glucosa en un cultivo por lotes alimentado para la producción de proteína verde de fluorescencia recombinante (GFP) en E. coli.
La parte computacional del sensor virtual utilizó ecuaciones cinéticas básicas y sumas para la estimación de tasas específicas y concentraciones totales de metabolitos. Se evaluaron dos estrategias de control para la alimentación del medio en el cultivo por lotes alimentado: (i) controlar las tasas específicas de metabolismo de desbordamiento y metabolitos de fermentación de ácidos mixtos en valores preestablecidos fijos, y (ii) controlar la concentración de la suma de estos metabolitos a un nivel establecido.
Los resultados indican que la última estrategia fue más eficiente para mantener un alto título y una baja variabilidad de la proteína verde de fluorescencia recombinante producida. El estudio presentado muestra cómo la variabilidad de un producto de proteína recombinante puede reducirse mediante el control basado en un sensor virtual. El sensor virtual reduce la necesidad de instrumentación y análisis fuera de línea. El principal objetivo de la Tecnología de Análisis en Proceso (PAT, por sus siglas en inglés), de aumentar la estabilidad del proceso y reducir la variabilidad de los parámetros clave del proceso, en particular el título del producto, se puede lograr con el enfoque del sensor virtual.
Además en la cromatografía líquida, se puede observar que el controlador no debe ser muy preciso (es decir, mostrar una rápida declinación, pequeños fallos estacionarios) para lograr una baja variabilidad en realidad.
Además, el resultado del estudio indica que el enfoque de control fisiológico no es necesariamente la estrategia de control más exitosa.
Sin embargo, sería deseable en la cromatografía líquida una mayor simplificación de la configuración del sensor virtual. Si un menor número de sensores de hardware puede lograr la estrategia de control, se mejoraría la aplicabilidad industrial y se reducirían aún más el mantenimiento y el suministro.
Nariz electrónica y espectroscopía NIR para el control de la producción de toxina del cólera
El NIR y la EN se utilizaron para monitorear y controlar un cultivo por lotes alimentado de Vibrio cholerae productor de la toxina del cólera B, realizado a escala de laboratorio y de producción.
Se desarrollaron un conjunto de modelos de predicción para biomasa en biorreactores, glucosa y acetato utilizando espectroscopía NIR, basados en la identificación espectral y la regresión PLS, lo que resultó en una alta correlación con los datos de referencia (errores estándar de predicción para biomasa, glucosa y acetato fueron 0.20 gl−1, 0.26 gl−1 y 0.28 gl−1).
Se integró un algoritmo de compensación para las perturbaciones en el biorreactor aireado en el cálculo del modelo, lo que mejoró especialmente la predicción del modelo de biomasa.
En primer lugar, los datos de NIR se aplicaron junto con los datos en línea de EN seleccionados por análisis de componentes principales (PCA) para generar una representación de trayectoria del cultivo por lotes alimentado.
Se demostró una correlación entre la progresión del cultivo y las señales de la Nariz Electrónica (EN), lo que resultó beneficioso para monitorear la calidad del cultivo.
Se mostró que una desviación del comportamiento normal del cultivo podía ser fácilmente reconocida y que la trayectoria podía alertar sobre una contaminación bacteriana. En segundo lugar, los datos de NIR indicaron el potencial de predecir la concentración de la toxina del cólera formada con un error de predicción del modelo de 0.020 g l−1.
En tercer lugar, la predicción en línea de la biomasa basada en el modelo NIR se utilizó para controlar la formación de acetato en el metabolismo de desbordamiento de la cultura de V. cholerae. El controlador comparó la tasa de crecimiento específica real, estimada a partir de la predicción, con la tasa crítica de crecimiento para la formación de acetato y, a partir de esa diferencia, ajustó la velocidad de alimentación de glucosa.
Estos cinco ejemplos están todos relacionados con la Tecnología de Análisis en Proceso (PAT), ya que aprovechan la operación en línea y utilizan conocimientos científicos sobre la cultura que se aplican en cálculos simples. Sin embargo, los parámetros del proceso derivados no son los más necesarios con urgencia.
Esto indica que hay una necesidad apremiante de aumentar la correspondencia entre los esfuerzos de investigación científica y las necesidades industriales relacionadas con PAT. Los requisitos metodológicos, tanto en términos instrumentales como en acceso a capacidad de modelado, parecen existir. Sin embargo, aún faltan validaciones exitosas de soluciones viables y rentables.
Sensores de temperatura en biorreactores de alimentación por lotes para la estimación de la tasa de crecimiento
En la imagen, dos sensores de temperatura en biorreactores miden la temperatura del medio de enfriamiento de entrada y salida con un cultivo de Escherichia coli que produce una proteína recombinante. Un tercer sensor mide la temperatura de un cultivo dentro del biorreactor.
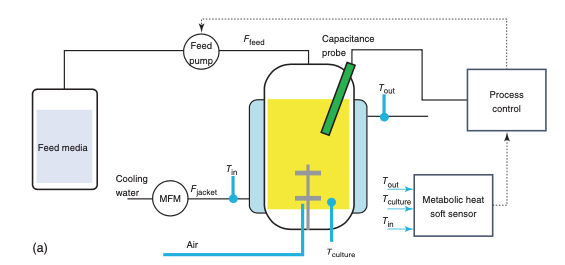
Las señales se utilizan en un conjunto de balances energéticos para estimar en línea la tasa de crecimiento específica durante toda la fase de alimentación por lotes. La alimentación de medios se controla a partir del valor estimado de 𝜇 en relación con un valor establecido de 𝜇. La figura muestra un detalle de un diagrama de control donde la alimentación se ajusta mediante un controlador PI para mantener el valor de 𝜇.
La estimación de 𝜇 puede convertirse fácilmente en concentración de biomasa. La ventaja de esta configuración es que la instrumentación con sensores de temperatura en biorreactores ya está presente; solo es necesario adquirir las señales e implementar el algoritmo.
La desventaja de este enfoque es que no solo el crecimiento genera calor en un cultivo de biorreactor, sino también la agitación, la aireación y la titulación. En consecuencia, esto debe compensarse correctamente. Si el calor metabólico es pequeño, la precisión se ve afectada.
Aplicando un filtrado secuencial de señales digitales, el sensor virtual se volvió más robusto para la práctica industrial con cultivos que generan bajo calor metabólico en entornos con niveles elevados de ruido. La señal estimada de la tasa de crecimiento específica obtenida a través del filtro secuencial de tres etapas permitió la alimentación controlada del sustrato durante la fase de alimentación por lotes del proceso de producción.
Las estimaciones de biomasa y tasa de crecimiento del sensor virtual también se compararon con una sonda de sensor en línea de capacitancia para las mismas variables. La comparación mostró una sensibilidad similar o mejor y una menor variabilidad para el sensor virtual de calor metabólico, lo que sugiere que el uso de sensores de temperatura en biorreactores permanentes, es una alternativa realista y económica para la monitorización y el control. Sin embargo, ambas alternativas son fáciles de implementar tanto en un sensor virtual solo como en paralelo.
Así, el estudio demuestra cómo el modelo de estimación puede implementarse como un sensor virtual en un software estándar de control de computadora, en paralelo con otras funciones de sensores virtuales, demostrando así un alto grado de operabilidad en entornos típicos de laboratorio o producción a pequeña escala.
Los resultados también muestran que el modelo del sensor virtual con la función de filtrado es comparable, e incluso mejor, que los sensores de hardware en línea alternativos para la concentración de biomasa y la tasa de crecimiento específica.
Titulación ácida-base para estimar la tasa de crecimiento en un biorreactor por lotes.
Se asume que existe una correlación directa entre la producción de H+ (iones hidrógeno) por parte de las células y el crecimiento. Por lo tanto, se registra el tiempo de funcionamiento de la bomba y la señal del electrodo de pH para el cultivo. Un algoritmo sencillo convierte las señales en biomasa. Si la suposición es correcta y no ocurren otros procesos generadores de H+ en el cultivo, la relación se mantiene.
Sin embargo, si el medio tiene una composición desconocida de aminoácidos, la correlación es más compleja. El ejemplo en la figura se toma de un cultivo donde el medio está definido. La correlación entre la muestra de referencia de biomasa y las estimaciones es alta en la región investigada. Nuevamente, la ventaja con el sensor virtual es que no se requiere ninguna instrumentación auxiliar; el sensor virtual se implementa directamente utilizando las señales existentes en un algoritmo agregado en el software de control del sistema del biorreactor.
El estudio se amplió con sensores de temperatura en biorreactores virtuales adicionales basados en datos en línea estándar de procesos de fermentación y modelos para otras variables de estado en procesos de alimentación por lotes de E. coli: la concentración de biomasa, la tasa de crecimiento específica, la capacidad de transferencia de oxígeno del biorreactor y el nuevo sensor RO/S, que es la relación entre el consumo de oxígeno y el sustrato energético. La variable RO/S crece continuamente en un cultivo de alimentación por lotes con alimentación constante de glucosa, lo que refleja la creciente demanda de mantenimiento con una tasa de crecimiento específica decreciente. El sensor RO/S también respondió a cambios rápidos en el pH, reflejando la creciente demanda de energía para el mantenimiento. Se sugiere que este sensor puede utilizarse para monitorear el grado de estrés fisiológico que demanda energía para la supervivencia.
Este estudio muestra que modelos simples pueden ser utilizados para obtener información adicional a partir de las variables estándar registradas en el proceso de fermentación. Las aplicaciones pueden ser tanto para la caracterización del proceso fuera de línea, como en este estudio, o para el control de retroalimentación en línea. Esto último aumenta la demanda de datos de medición primarios o la necesidad de filtrado de datos en línea. Los sensores pueden ser bastante sensibles a errores en los datos de entrada bajo ciertas condiciones, pero esto genera un error sistemático en los valores de salida y no debería impedir su uso para monitorear cambios en el rendimiento del proceso.
- Optimización en biorreactores del medio para producción de células
- Optimización de Medios de Cultivo Celular para la Producción Máxima de Proteínas
- Optimización de Cultivos Microbianos para una Producción Máxima
- Diseño de experimentos y biorreactores (DoE)
- Comparación de métodos DoE para la optimización de la producción en biorreactores

